On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method
by Antun Skuric, Vincent Padois, Nasser Rezzoug, David Daney
Published in IEEE ICRA2022 & IEEE RA-L, 2022
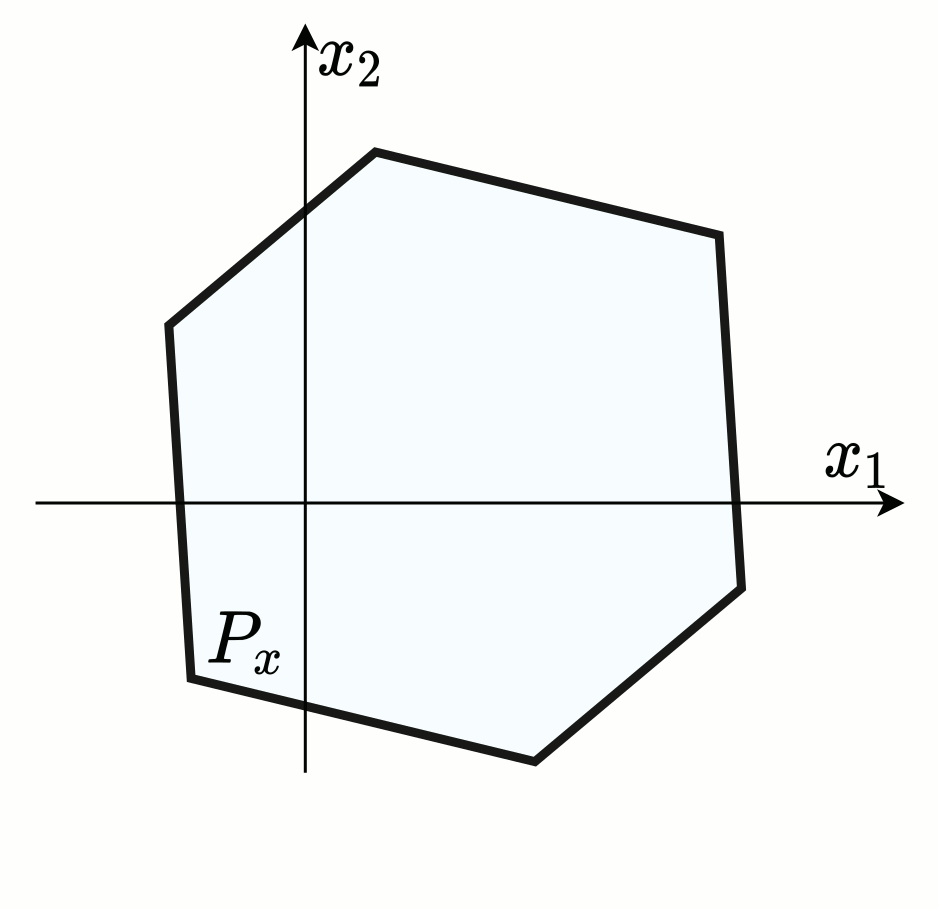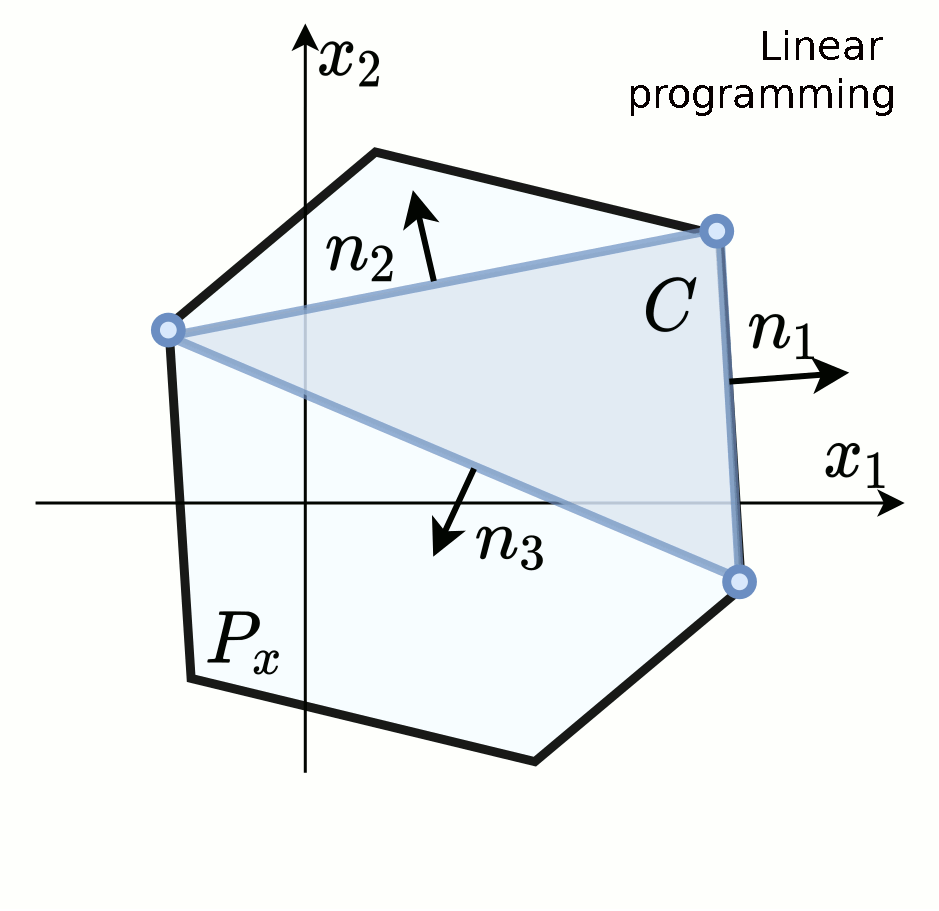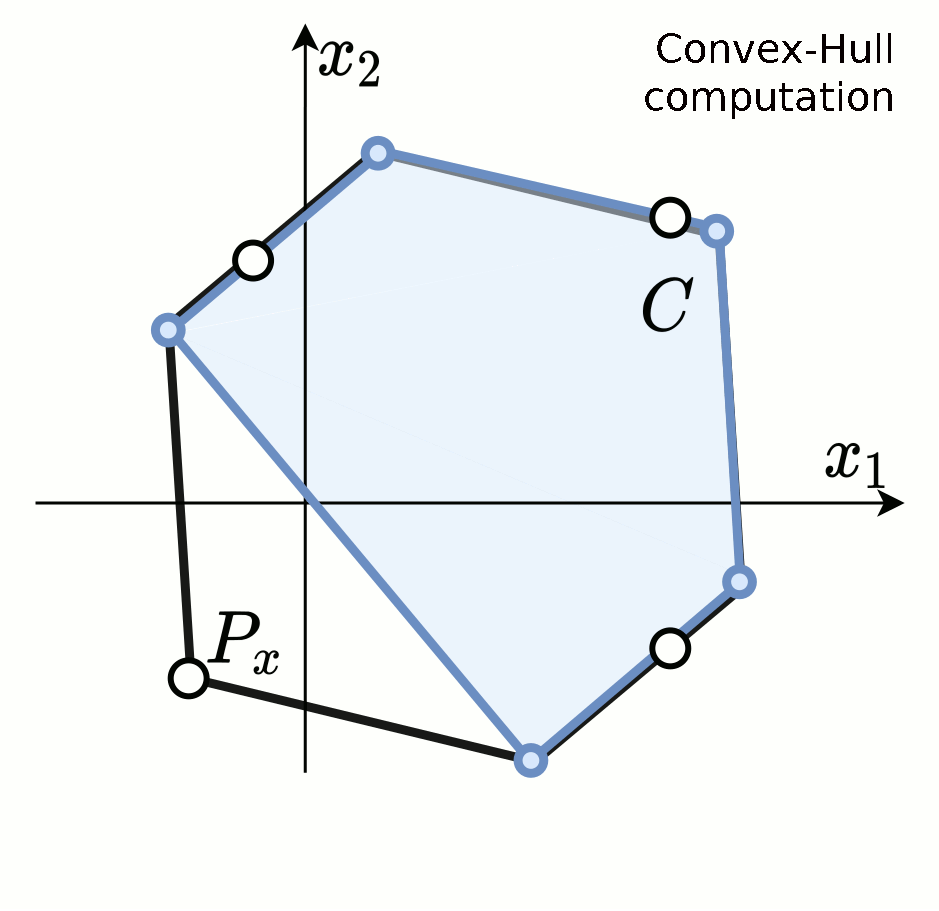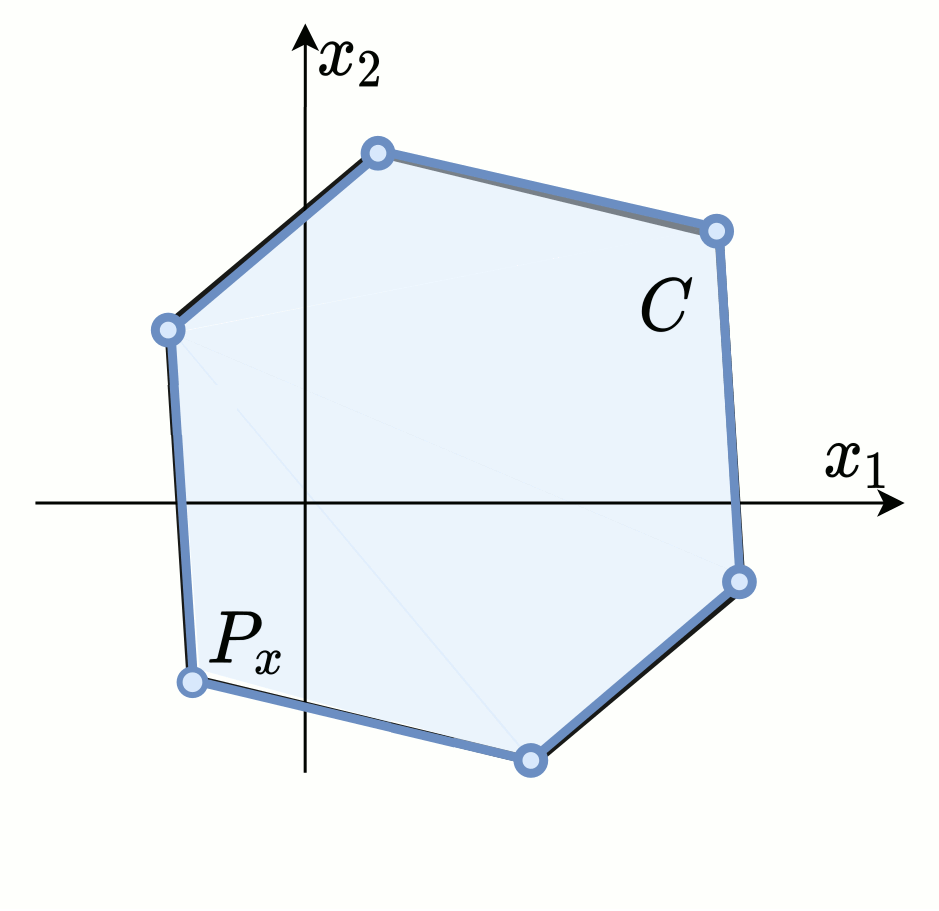Iterative convex hull is a polytope evaluation algorithm developed for the generic class of the linear algebra problems:
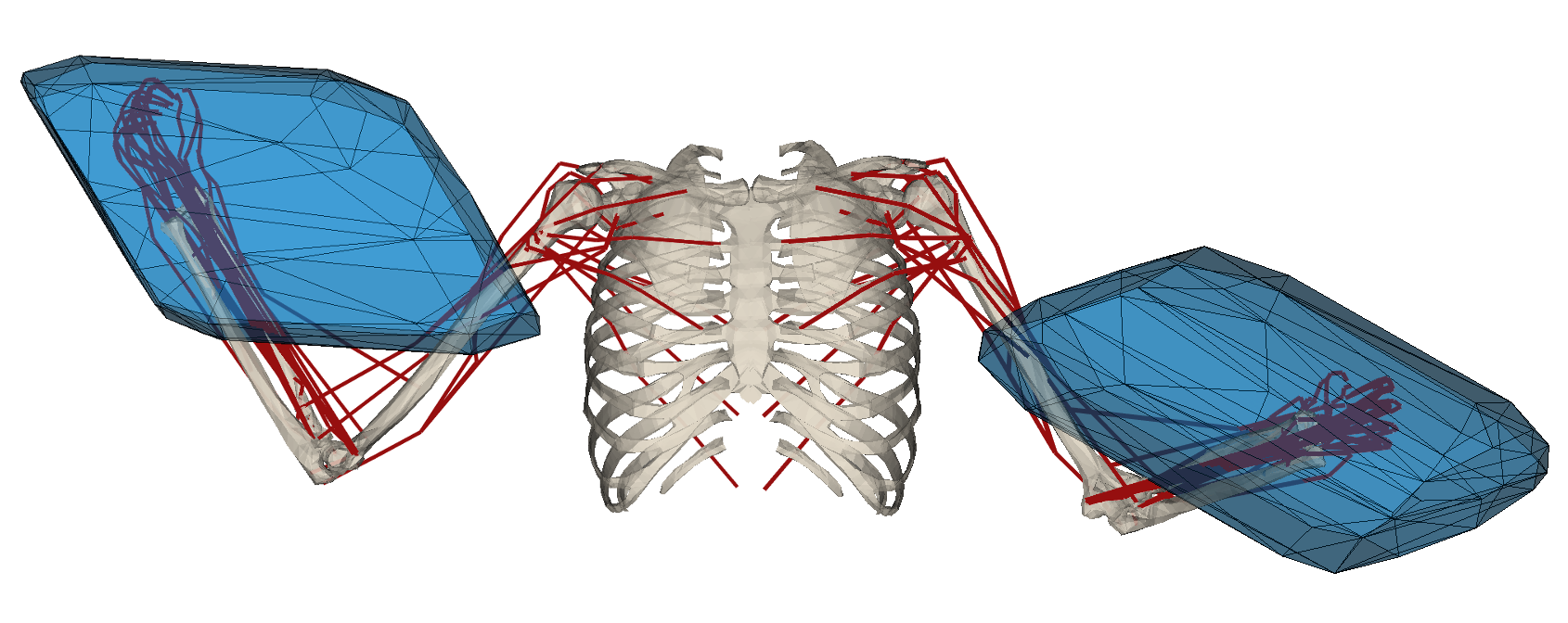
This type of problems can be found in many different domains, one of them being the wrench capacity analysis of the human musculoskeletal models. In this paper the method overview is given as well as the verified on the assistive robotics scenario.
Paper Abstract
Many recent human-robot collaboration strategies, such as Assist-As-Needed (AAN), are promoting humancentered robot control, where the robot continuously adapts its assistance level based on the real-time need of its human counterpart. One of the fundamental assumptions of these approaches is the ability to measure or estimate the physical capacity of humans in real-time.In this work, we propose an algorithm for the feasibility set analysis of a generic class of linear algebra problems. This novel iterative convex-hull method is applied to the determination of the feasible Cartesian wrench polytope associated to a musculoskeletal model of the human upper limb.
The method is capable of running in real-time and allows the user to define the desired estimation accuracy. The algorithm performance analysis shows that the execution time has near-linear relationship to the considered number of muscles, as opposed to the exponential relationship of the conventional methods. Finally, real-time robot control application of the algorithm is demonstrated in a Collaborative carrying experiment, where a human operator and a Franka Emika Panda robot jointly carry a 7kg object. The robot is controlled in accordance to the AAN paradigm maintaining the load carried by the human operator at 30% of its carrying capacity.
The full version of the paper is open access and can be found in HAL database: manuscript
Video presentation
Getting started
Matlab and python code and more documentation about practical implementation of this method can be found on our gitlab.
Additionally the full algorithm has been implemented in the python pip package [pycapacity](https://auctus-team.github.io/ask-space capacity metrics for robots and human manipulators in real-time.
pip install pycapacity
Example code
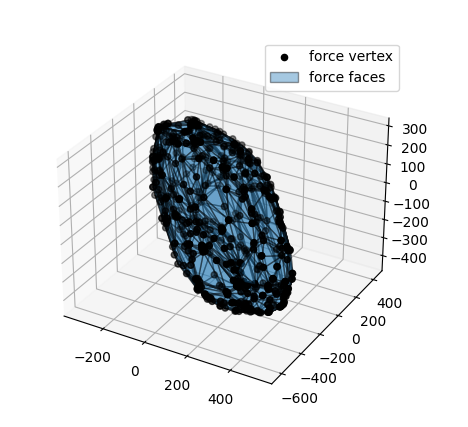
Example code for randomised 20 muscle human musculoskeltal model using the pycapacity package
"""
A simple example program for 3d force polytope
evaluation of a randomised 20 muscle 6dof
human musculoskeletal model
"""
import pycapacity.human as capacity # robot capacity module
import numpy as np
L = 20 # number of muscles
m = 3 # 3d forces
n = 6 # number of joints - dof
# this seed is used to generate the same image
# as in the examples in the docs
np.random.seed(123456)
J = np.array(np.random.rand(m,n))*2-1 # random jacobian matrix
N = np.array(np.random.rand(n,L))*2-1 # random moment arm matrix
F_max = 100*np.ones(L) # muscle forces limits max and min
F_min = np.zeros(L)
f_poly = capacity.force_polytope(J,N, F_min, F_max, 0.1) # calculate the polytope
# plotting the polytope
import matplotlib.pyplot as plt
from pycapacity.visual import * # pycapacity visualisation tools
fig = plt.figure(4)
# draw faces and vertices
plot_polytope(plot=plt,
polytope=f_poly,
label='force',
edge_color='black',
alpha = 0.4)
plt.legend()
plt.show()
When executed you’ll be able to see the 3D plot of the polytope
